Simulating flocks of birds
The Boids (short for “bird-like-objects”) algorithm was invented by Craig W. Reynolds in 1986 to simulate the movement of flocks of birds. One of the key insights was that a bird in a flock may be simulated using three simple rules:
- Collision Avoidance: avoid collisions with nearby flockmates
- Velocity Matching: attempt to match velocity with nearby flockmates
- Flock Centering: attempt to stay close to nearby flockmates
Using these simple rules, a very realistically looking simulation of flocks of birds may be implemented. It is usually done in two or three dimensions, but may in principle be done in any space where direction and distance can be defined meaningfully, for example a normed vector space.
Using the simulation to compose music
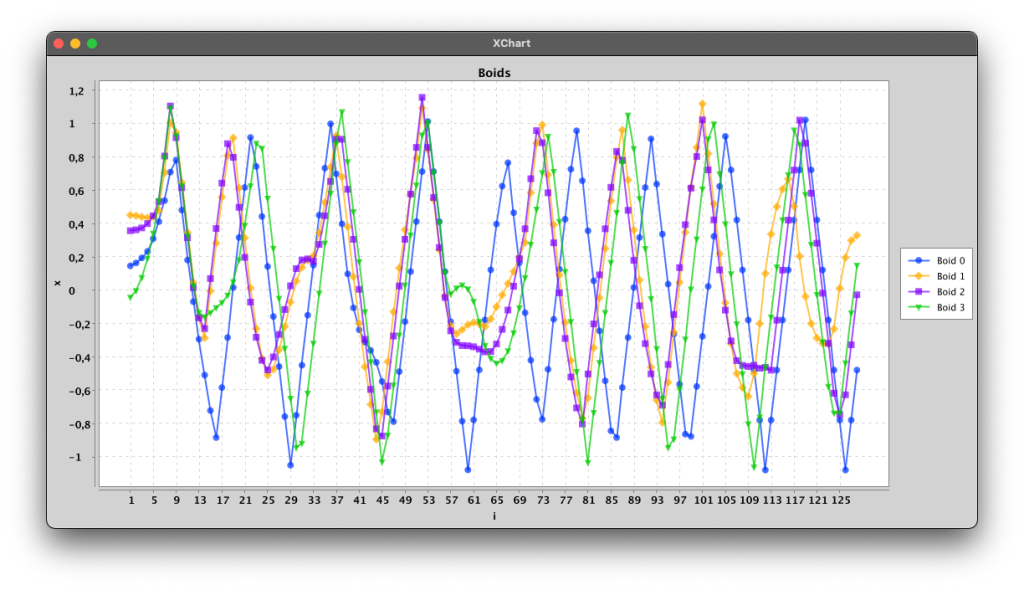
We have created a special-purpose version of the boids algorithm to compose music. In this, we limit the boids to move around in one dimension but use the same rules as in simulations in two or three dimensions. Each boid corresponds to a voice and the one-dimensional space is mapped to a set of notes in a diatonic scale. The rules are adjusted such that the collision avoidance prefers a distance of at least a third, but since there are other rules influencing the movement, and only one dimension to move around in, the boids collide often. We also add rules to keep the boids in a certain range. Left on their own, the boids tend to land in an equilibrium, so to ensure an interesting dynamic, we let one boid move randomly with its velocity changing according to a brownian motion (Boid 0 in the plot below) as well as the other rules, the boids are following. With four boids this gives a result as shown below:
The voices are mapped to notes (MIDI-files) and was used in the recording all three tracks of the album “Pieces of infinity 02” by Morten Bach and Jonas Lindstrøm. The algorithm was changed slightly, for example to allow some boids to move faster than others, or to allow more boids, but the base algorithm is the same used to generate all voices for the three tracks.
References
Reynolds, Craig (1987): Flocks, herds and schools: A distributed behavioural model. SIGGRAPH ’87: Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques, https://team.inria.fr/imagine/files/2014/10/flocks-hers-and-schools.pdf
Lindstrøm, Jonas (2022): boid-composer, https://github.com/jonas-lj/boid-composer